Weibull Distribution is a continuous probability distribution that is used to model survival time, failure time and related events. This distribution is based on the Weibel probability distribution function, which was introduced by Waldemar Weibel in the 1951s.
What is Weibel distribution?
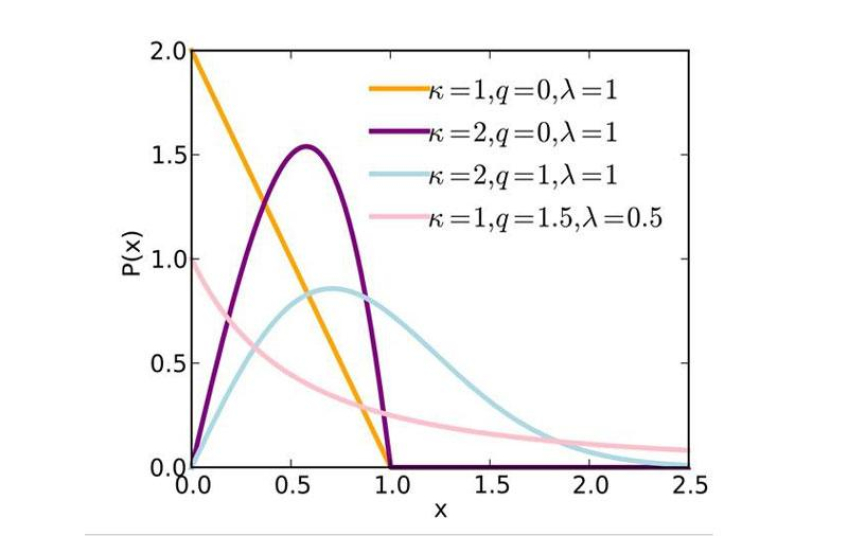
The Weibull distribution is a continuous probability distribution used to model lifetime and failure time. This distribution has high flexibility and can model a wide range of failure behaviors including premature failures, wear-out and random failures. Weibull distribution parameters include shape and scale. The shape parameter determines the shape of the distribution and the scale parameter determines the scale of the distribution. Weibel distribution is used in various fields such as engineering, life sciences and economics. The applications of this distribution should be mentioned in the field of engineering (for predicting the useful life of parts and equipment), biological sciences (for modeling the life span of living organisms), economics (for modeling the bankruptcy time of companies), etc. This distribution provides us with a number of key advantages, the first of which is high flexibility. The Weibull distribution can model a wide range of failure behaviors. Weibel distribution is easy to understand and use, which makes it useful in various fields. However, the Weibull distribution also has disadvantages. The first one is difficult to interpret. Weibull distribution parameters are difficult to interpret. The Weibull distribution is sensitive to its parameters. However, the Weibull distribution is a powerful tool for modeling lifetime and failure time. The Weibull distribution is defined as follows:
f(x;λ,k)={λk(λx)k−1exp[−(λx)k]0x≥0,x<0,
In this function, lambda is the scale parameter and k is the shape parameter. The lambda parameter indicates the scale of the distribution and its value must be greater than zero. The parameter k indicates the slope of the distribution and its value can be any real number greater than zero. Due to the ability to adjust the scale and shape, the Weibel distribution can display various types of distributions, including exponential distribution (k=1), Rayleigh distribution (k<1) and Rice distribution (k>1).
Among the features of the Weibel distribution index, the following three items should be mentioned.
Limiting the negativity of the distribution function to non-negative numbers.
It is a decreasing distribution function that represents the decrease in the probability of an event with an increase in the value of the random variable.
If k=1, Weibel distribution becomes exponential distribution.
The Weibull distribution is used in many areas of engineering and basic science and can be well used to model survival and failure times in predictive and experimental studies.
Three-parameter Weibull distribution
Three-Parameter Weibull Distribution is a continuous probability distribution that is defined based on the Weibull probability distribution function with three main parameters. This distribution acts as a more flexible distribution than the Two-Parameter Weibull Distribution and allows the shape of the distribution to better fit the data. The probability distribution function of the three-parameter Weibull distribution is defined as follows:
f(x;λ,k,γ)={λk(λx−γ)k−1exp[−(λx−γ)k]0x≥γ,x<γ,
In this function, λ is the scale parameter, k is the shape parameter, and γ is the displacement parameter. The parameter λ indicates the scale of the distribution and its value must be greater than zero. The parameter k indicates the slope of the distribution and its value can be any real number greater than zero. The parameter γ also controls the change of distribution location and its value can be any real number. By changing the values of these three parameters, the three-parameter Weibull distribution can display various types of distributions, including exponential distribution (k=1), Rayleigh distribution (k<1) and Rice distribution (k>1). Also, by using the parameter γ, it is possible to adjust the distribution location. The three-parameter Weibull distribution can be used in modeling more complex and realistic problems and allows for a better fit with real data.
Weibull Distribution is a continuous probability distribution that is used to model survival time, failure time and related events. This distribution is based on the Weibel probability distribution function, which was introduced by Waldemar Weibel in the 1951s.
What is Weibel distribution?
The Weibull distribution is a continuous probability distribution used to model lifetime and failure time. This distribution has high flexibility and can model a wide range of failure behaviors including premature failures, wear-out and random failures. Weibull distribution parameters include shape and scale. The shape parameter determines the shape of the distribution and the scale parameter determines the scale of the distribution. Weibel distribution is used in various fields such as engineering, life sciences and economics. The applications of this distribution should be mentioned in the field of engineering (for predicting the useful life of parts and equipment), biological sciences (for modeling the life span of living organisms), economics (for modeling the bankruptcy time of companies), etc. This distribution provides us with a number of key advantages, the first of which is high flexibility. The Weibull distribution can model a wide range of failure behaviors. Weibel distribution is easy to understand and use, which makes it useful in various fields. However, the Weibull distribution also has disadvantages. The first one is difficult to interpret. Weibull distribution parameters are difficult to interpret. The Weibull distribution is sensitive to its parameters. However, the Weibull distribution is a powerful tool for modeling lifetime and failure time. The Weibull distribution is defined as follows:
f(x;λ,k)={λk(λx)k−1exp[−(λx)k]0x≥0,x<0,
In this function, lambda is the scale parameter and k is the shape parameter. The lambda parameter indicates the scale of the distribution and its value must be greater than zero. The parameter k indicates the slope of the distribution and its value can be any real number greater than zero. Due to the ability to adjust the scale and shape, the Weibel distribution can display various types of distributions, including exponential distribution (k=1), Rayleigh distribution (k<1) and Rice distribution (k>1).
Among the features of the Weibel distribution index, the following three items should be mentioned.
Limiting the negativity of the distribution function to non-negative numbers.
It is a decreasing distribution function that represents the decrease in the probability of an event with an increase in the value of the random variable.
If k=1, Weibel distribution becomes exponential distribution.
The Weibull distribution is used in many areas of engineering and basic science and can be well used to model survival and failure times in predictive and experimental studies.
Three-parameter Weibull distribution
Three-Parameter Weibull Distribution is a continuous probability distribution that is defined based on the Weibull probability distribution function with three main parameters. This distribution acts as a more flexible distribution than the Two-Parameter Weibull Distribution and allows the shape of the distribution to better fit the data. The probability distribution function of the three-parameter Weibull distribution is defined as follows:
f(x;λ,k,γ)={λk(λx−γ)k−1exp[−(λx−γ)k]0x≥γ,x<γ,
In this function, λ is the scale parameter, k is the shape parameter, and γ is the displacement parameter. The parameter λ indicates the scale of the distribution and its value must be greater than zero. The parameter k indicates the slope of the distribution and its value can be any real number greater than zero. The parameter γ also controls the change of distribution location and its value can be any real number. By changing the values of these three parameters, the three-parameter Weibull distribution can display various types of distributions, including exponential distribution (k=1), Rayleigh distribution (k<1) and Rice distribution (k>1). Also, by using the parameter γ, it is possible to adjust the distribution location. The three-parameter Weibull distribution can be used in modeling more complex and realistic problems and allows for a better fit with real data.
What are the uses of Weibel distribution?
Weibel distribution is used in various sciences and in many fields. The first is medical science. Weibel distribution can be used in survival time modeling to check the life of patients, check the life of medical parts and analyze errors. This distribution can well describe the decreasing behavior of the exponential distribution function and the shape of the Weibel distribution in medical and biological phenomena. In engineering, the Weibull distribution is used as a useful tool in modeling the lifetime of pipelines, electrical and mechanical systems, electronic components, and manufacturing and assembly systems. This distribution can help to analyze the behavior of parts reduction and predict their life.
Weibel distribution can be used in buyer behavior modeling, product and project performance analysis, delivery time modeling and supply chain management. For example, in modeling the time required to deliver orders, the Weibull distribution can describe the delivery time behavior well. Social science professionals can use Weibel distribution in modeling social events and processes, modeling presence time in industrial and service systems, etc. In general, the Weibel distribution with its diverse properties is a powerful tool for modeling complex behaviors and analyzing data that simultaneously has the property of reducing the exponential distribution function and the shape of the Weibel distribution.
An example of Weibel distribution in the world of engineering
A real example of using the Weibull distribution in the field of engineering can be related to modeling the life of pipelines. Suppose an oil and gas company has thousands of kilometers of pipelines to transport materials and fuels in different regions. The useful life of these pipelines decreases over time and they require maintenance. To model the lifetime of pipelines and predict maintenance time, Weibull distribution can be used. This distribution can describe the decreasing behavior of the exponential distribution function according to the specific characteristics of pipelines (such as gender, age, weather conditions and use).
Using data collected over time, we can estimate the parameters of the Weibull distribution. The lambda parameter indicates the average survival time or the average life of the pipelines, while the K parameter indicates the shape of the Weibel distribution and the rate of change in the life time of the pipelines. By analyzing this distribution, we can obtain useful information, such as the average life time of pipelines, the percentage of lines that need repair in a certain time period, as well as information about changes in the life of pipelines over time.
Using this information, the company can formulate optimal maintenance plans for the pipelines, plan the expected repair time and take advantage of the better life and performance of the pipelines. Therefore, the Weibull distribution in this example can help us model the lifetime of pipelines and formulate optimal maintenance plans.